Vanadis – model rozprzestrzeniania siДҷ zanieczyszczeЕ„ w atmosferze
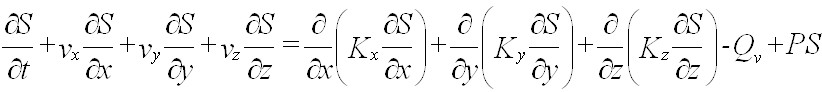
W rozwiД…zaniu zastosowana jest metoda Eulera, w której ukЕӮad wspóЕӮrzДҷdnych i siatka elementów skoЕ„czonych zwiД…zane sД… ze ЕәródЕӮem zanieczyszczenia.
Zanieczyszczenie przemieszcza siДҷ wzglДҷdem siatki z prДҷdkoЕӣciД… vx, vy, vz . PrzyjДҷty sposób dyskretyzacji obszaru za pomocД… elementów oЕӣmiowДҷzЕӮowych i trójkД…tnych zobrazowany jest na poniЕјszym rysunku
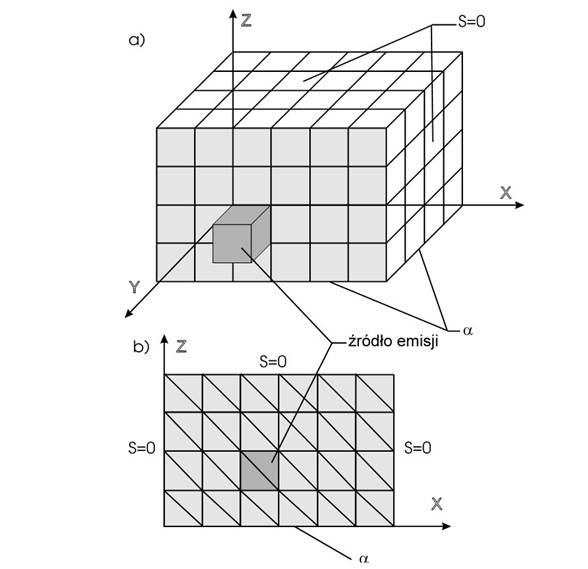
Dyskretyzacja obszaru trójwymiarowego (a) za pomocД… elementów oЕӣmiowДҷzЕӮowych oraz obszaru dwuwymiarowego (b) za pomocД… elementów trójkД…tnych
W wyniku odpowiedniego podziaЕӮu obszaru na elementy uwzglДҷdniona zostaje topografia terenu. RozwiД…zanie równania dyfuzji metodД… elementów skoЕ„czonych w przestrzeni trójwymiarowej polega na okreЕӣleniu pola stДҷЕјeЕ„ w wДҷzЕӮach elementów.
Warunki brzegowe i parametry modelu
Równanie dyfuzji rozwiД…zywane jest przy przyjДҷciu na czДҷЕӣci powierzchni obszaru warunku brzegowego pierwszego rodzaju S(x,y,z)=0
Warunek ten zakЕӮada caЕӮkowity zanik zanieczyszczenia w duЕјej odlegЕӮoЕӣci od ЕәródЕӮa emisji. Natomiast przyjДҷcie warunku brzegowego róЕјnego od zera (S(x,y,z)>0) równoznaczne jest z uwzglДҷdnieniem tЕӮa zanieczyszczenia.
Na powierzchni ziemi zanieczyszczenie jest pochЕӮaniane; gДҷstoЕӣДҮ pochЕӮanianego strumienia zanieczyszczeЕ„ jest proporcjonalna do wspóЕӮczynnika wnikania (prДҷdkoЕӣДҮ suchego osiadania).
W caЕӮej objДҷtoЕӣci zanieczyszczenie ulega rozpadowi z czasem poЕӮowicznego zaniku ln2/P (wspóЕӮczynnik zaniku P moЕјe byДҮ funkcjД… stДҷЕјenia zanieczyszczenia, funkcjД… poЕӮoЕјenia i czasu oraz warunków meteorologicznych, umoЕјliwia to uwzglДҷdnienie reakcji chemicznych, opadów i wszystkich tych czynników, które wpЕӮywajД… na rozpad, bД…dЕә teЕј powstawanie zanieczyszczeЕ„). W wybranych elementach umieszczone jest ЕәródЕӮo zanieczyszczenia o objДҷtoЕӣciowym natДҷЕјeniu emisji Qv
Numeryczne rozwiД…zanie równania transportu masy napotyka na trudnoЕӣci zwiД…zane z wystДҷpowaniem czЕӮonu konwekcji, który moЕјe powodowaДҮ do rozwiД…zaЕ„ oscylacyjnych. Otrzymanie zadowalajД…cych wyników moЕјe byДҮ osiД…gniДҷte poprzez zmniejszenie wymiarów siatki elementów lub przez zastosowanie metody reszt waЕјonych z niesymetrycznymi funkcjami wagi. W tym rozwiД…zaniu zastosowaЕӮem metodДҷ Galerkina.
Obliczanie wartoЕӣci elementów skЕӮadajД…cych siДҷ na ukЕӮad równaЕ„ liniowych jest realizowane metodД… Gaussa. UkЕӮad równaЕ„ rozwiД…zany jest metodД… gradientów sprzДҷЕјonych.
PrzykЕӮadowe obliczenia (dane z pliku konfiguranyjnego vanadis.cfg):
Q[kg/s] K[m^2/s] P[1/s] V1[m/s] V2[m/s] V3[m/s] ALPHA[m/s]
*********************************************************************************
0 1 2 3 4 5 6 7 8
012345678901234567890123456789012345678901234567890123456789012345678901234567890
*********************************************************************************
+001.00E+00 +040.00E+00 +07.00E-04 +00.00E+00 -00.00E+00 +01.50E+00 +01.00E-03
Q[kg/s] K[m^2/s] P[1/s] V1[m/s] V2[m/s] V3[m/s] ALPHA[m/s]
*********************************************************************************
0 1 2 3 4 5 6 7 8
012345678901234567890123456789012345678901234567890123456789012345678901234567890
*********************************************************************************
+001.00E+00 +040.00E+00 +07.00E-04 +00.00E+00 -00.00E+00 +00.00E+00 +01.00E-03
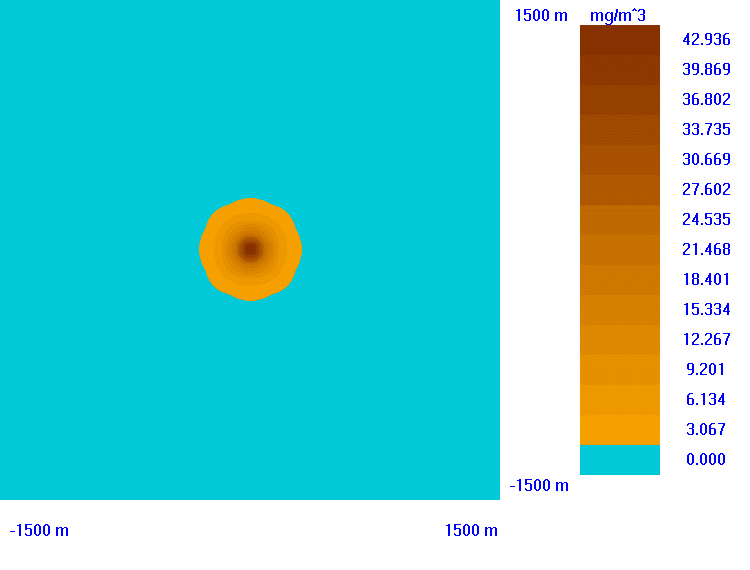
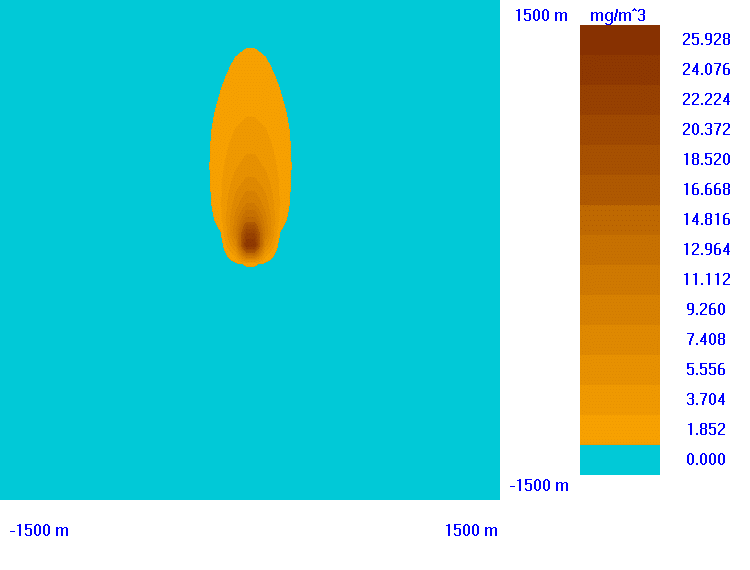
Porównanie modelu trójwymiarowego z modelem Pasquilla
W celu porównania modeli przeprowadziЕӮem obliczenia rozprzestrzeniania siДҷ zanieczyszczeЕ„ wokóЕӮ ЕәródЕӮa emisji.
RozwiД…zanie Pasquilla opracowaЕӮem w oparciu o „Wytyczne obliczania stanu zanieczyszczenia powietrza atmosferycznego Ministerstwo Ochrony Еҡrodowiska, Zasobów Naturalnych i LeЕӣnictwa, 1993” autorstwa J. Iwanka.
W rozwiД…zaniu Pasquilla przyjДҷte sД… nastДҷpujД…ce dane:
· natДҷЕјenie emisji 1 g/s
· poЕӮoЕјenie ЕәródЕӮa emisji X=0, Y=0, H=60 m
· typ równowagi atmosfery 4
· Еӣrednia prДҷdkoЕӣДҮ wiatru 1.55 m/s
· czas poЕӮowicznego zaniku zanieczyszczenia 1000 s
· szorstkoЕӣДҮ terenu 1.5 m

RozkЕӮad zanieczyszczeЕ„ otrzymany modelem Pasquilla w pЕӮaszczyЕәnie XY dla Z=0 (a) oraz w pЕӮaszczyЕәnie YZ dla X=900m (b); vy=0
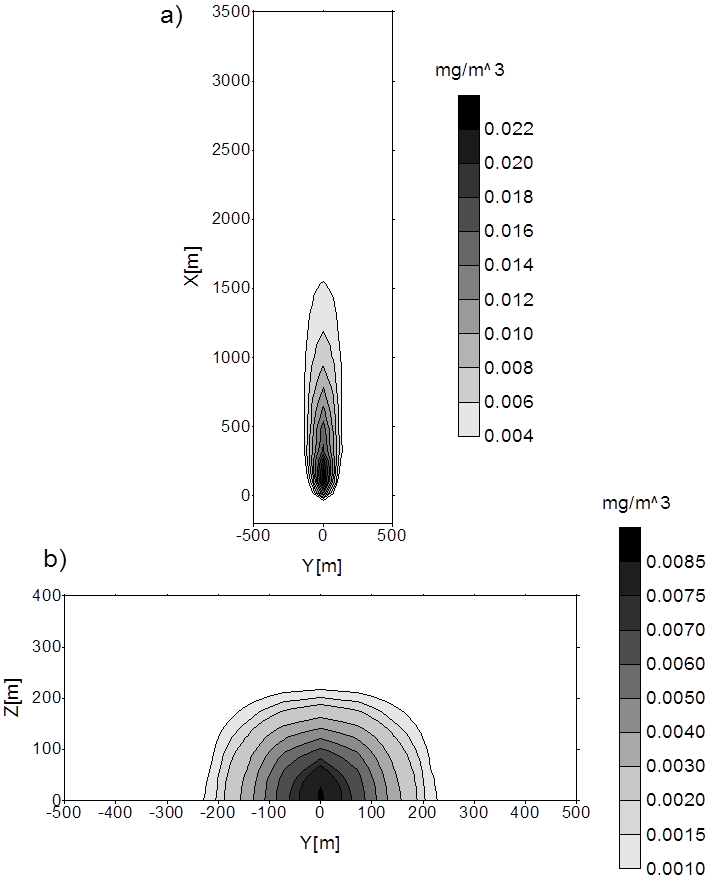
RozkЕӮad zanieczyszczeЕ„ otrzymany metodД… elementów skoЕ„czonych w pЕӮaszczyЕәnie XY dla Z=0 (a) oraz w pЕӮaszczyЕәnie YZ dla X=900m (b); vy=0

